Rozkład normalny

Definicje rozkład normalny (krzywa Gaussa) jest najważniejszym rozkładem zmiennej w statystyce, ponieważ wiele cech występujących w naturze, jak i zjawisk społecznych ma właśnie taki rozkład, np. wzrost, waga , iloraz inteligencji. Rozkład normalny charakteryzują dwa parametry – wartość oczekiwana (średnia arytmetyczna) i odchylenie standardowe. Zmienna losowa x ma rozkład normalny o parametrach m i s jeśli jej funkcja gęstości prawdopodobieństwa ma postać:

Wykresem funkcji gęstości rozkładu normalnego jest krzywa Gaussa

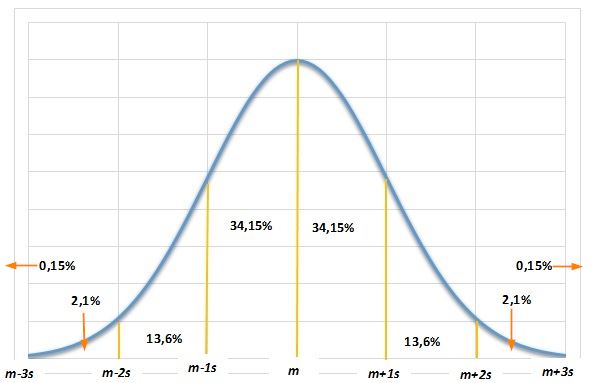
Kształt rozkładu wskazuje na to, że wartości koncentrują się wokół średniej, im bliżej krańców rozkładu, tym mniejsza liczebność przypadków. Zjawisko to opisuje reguła trzech sigm. Reguła ta mówi, że większość przypadków 68,3% leży w odległości +/- 1 odchylenie standardowe od średniej, w odległości +/- dwóch odchyleń standardowych od średniej znajduje się 95,5% przypadków, w zakresie +/- trzech odchyleń standardowych od średniej 99,7% przypadków. Poza trzecim odchyleniem standardowym znajduje się 3% przypadków, przypadki te często są traktowane jako odstające (outliery), a pojawienie się w zbiorze danych ich skutkuje komplikacjami w szczególności przy stosowaniu parametrycznych metod statystycznych, np. metoda najmniejszych kwadratów.

Sformalizowany zapis reguły trzech sigm jest następująco:

Własności rozkładu normalnego:

• Wartość oczekiwana (średnia), mediana i dominanta leżą w tym samym punkcie (są sobie równe)
• Dla x = m (tj. w punkcie średniej arytmetycznej) krzywa osiąga maksimum równe 
• Krzywa ma dwa punkty przegięcia dla x=m-1s oraz x=m+1s
• Krzywa jest symetryczna względem prostej  x=m

Bibliografia

King, B., M., Minium, E., W. (2009). Statystyka dla psychologów i pedagogów. Warszawa: PWN

Wasilewska, E. (2015). Statystyka matematyczna. Warszawa: Wyd. Diffin